Overview

V-Ray uses Deterministic Monte Carlo (DMC) — a variant of Monte Carlo sampling (MC) method for evaluating "blurry" values (anitaliasing, depth of field, indirect illumination, area lights, glossy reflections/refractions, translucency, motion blur, etc.).

The actual number of samples for the DMC sampler's blurry values are determined by three factors:

• The subdivs value for a particular blurry effect. This is multiplied by the Global subdivs multiplier.

• The importance of the value (for example, dark glossy reflections can do with fewer samples than bright ones, since the effect of the reflection on the final result is smaller; distant area lights require fewer samples than closer ones, etc.). Basing the number of samples allocated for a value on importance is called importance sampling.

• The variance (think "noise") of the samples taken for a particular value - if the samples are not very different from each other, then the value can do with fewer samples; if the samples are very different, then a larger number of them will be necessary to get a good result. This basically works by looking at the samples as they are computed one by one and deciding, after each new sample, if more samples are required. This technique is called early termination or adaptive sampling.

The difference between pure Monte Carlo sampling and Deterministic Monte Carlo is that the first uses pseudo-random numbers which are different for each and every evaluation (and so re-rendering a single image will always produce slightly different results in the noise), while Deterministic Monte Carlo uses a pre-defined set of samples (possibly optimized to reduce the noise), which allows re-rendering an image to always produce the exact same result. By default, the Deterministic Monte Carlo method used by V-Ray is a modification of Schlick sampling, introduced by Christophe Schlick.

V-Ray is an adaptive sampling engine. This means that whenever V-Ray needs to compute a value, like the color of a pixel, or the light reflected from a surface, V-Ray will take a varying number of samples for that value, depending on the context. The adaptive algorithm that V-Ray uses is very straightforward: for any effect that requires several samples, V-Ray first computes a small amount of samples, and then, if the variance of the samples is too big, it continues to take more samples until the result is good enough.

The samples that V-Ray needs to compute can be broadly classified as image samples and shading samples. Image samples are those directly related to pixel values that compose the final image, including depth of field and motion blur effects. Shading samples are those taken to compute effects like glossy reflections, global illumination, area lights, etc. V-Ray employs adaptive sampling in both of these cases. The picture below shows one possible way that a light or a material may be sampled within a given pixel.

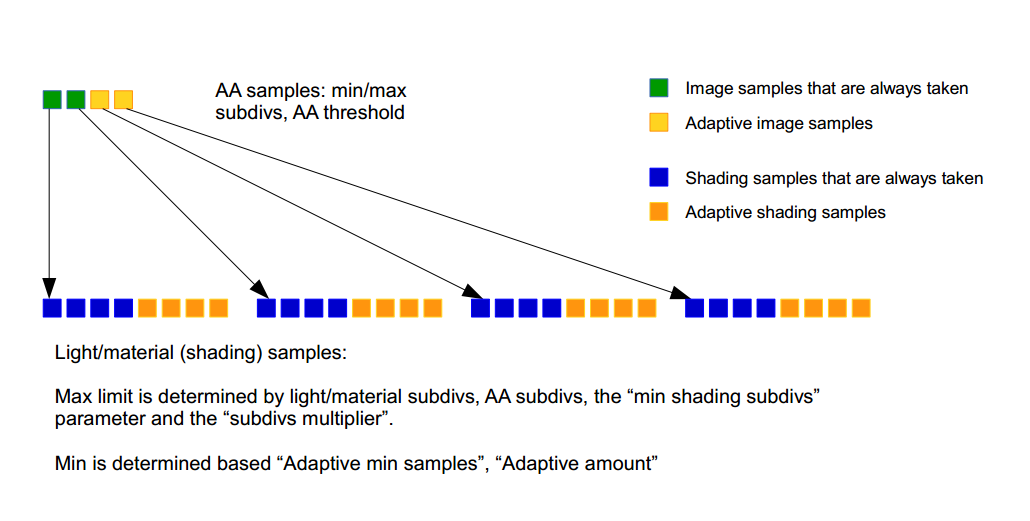
For each value that must be sampled adaptively, there is a certain minimum number of samples that V-Ray always computes, a maximum number of samples, and a noise threshold that controls how many samples between the minimum and the maximum would be actually computed. The minimum number of samples are needed because, like every adaptive algorithm, V-Ray's DMC sampler needs to gather a bit of information about the particular value that is being sampled before it can make any assumptions about it.

For image sampling, the three values - minimum samples, maximum samples and noise threshold - are directly specified by the user. The VRaySampleRate render element can show how many samples were actually performed, as percentage of the maximum. However for shading effects like glossy reflections, area lights, GI, it would be too cumbersome to have to specify the three values for each effect separately. To simplify the setup, V-Ray allows the user to specify the maximum number of samples using the various subdivs¹ parameters for lights, materials and so on (although importance sampling may modify this maximum number depending on the expected contribution of the value). The noise threshold is specified globally for all values with the DMC noise threshold². What remains then, is to figure out the number of minimum samples that must be taken for a given value:

The minimum number of samples may be specified directly with a fixed number. This is not a bad approach, however it means that increasing the subdivs value for a shading effect might not always lead to improved quality, contrary to what users typically expect.

The minimum number of samples could be specified as percentage of the maximum number of samples. This approach ensures that increasing the subdivs value always results in better quality, but if the maximum number of samples are too low to begin with, it may mean that there is not enough information in those samples for the adaptive algorithm to work reliably.

The V-Ray DMC sampler combines both strategies and takes the bigger value to determine the actual minimum number of samples. Those strategies are controlled by the DMC min². samples parameter and the DMC adaptive amount² parameter respectively. Once the minimum number of samples are taken, the DMC sampler continues taking more samples either until the noise threshold is reached, or the maximum number of samples are taken.

To disable any kind of adaptive sampling for shading effects, set the DMC adaptive amount² to 0.0. This can be done by using Max Script in V-Ray 5.

Notes

1 – The Subdivs parameters for lights and materials are hidden from the UI with V-Ray 5. VRayDirt and VRayCurvature have their own Subdivs parameters which work independently from the Adaptive sampling settings.

2 – These parameters are hidden from the UI in V-Ray 5. The most optimal values for them are set by default and they do not need to be changed in the majority of setups. They can be modified with max script.

References

More information on deterministic Monte Carlo sampling for computer graphics can be found from the sources listed below.

[1] C. Schlick, An Adaptive Sampling Technique for Multidimensional Integration by Ray Tracing, in Second Eurographics Workshop on Rendering (Spain), 1991, pp. 48-56
Describes deterministic MC sampling for antialiasing, motion blur, depth of field, area light sampling and glossy reflections.

[2] K. Chiu, P. Shirley and C. Wang, Multi-Jittered Sampling, in Graphics Gems IV, 1994
Describes a combination of jittered and N-rooks sampling for the purposes of computer graphics.

[3] Masaki Aono and Ryutarou Ohbuchi, Quasi-Monte Carlo Rendering with Adaptive Sampling, IBM Tokyo Research Laboratory Technical Report RT0167, November 25, 1996, pp.1-5
An online version can be found at
http://www.kki.yamanashi.ac.jp/~ohbuchi/online_pubs/eg96_html/eg96.htm
Describes an application of low discrepancy sequences to area light sampling and the global illumination problem.

[4] M. Fajardo, Monte Carlo Raytracing in Action, in State of the Art in Monte Carlo Ray Tracing for Realistic Image Synthesis, SIGGRAPH 2001 Course 21, pp. 151-162;
An online version can be found at
http://cseweb.ucsd.edu/~viscomp/classes/cse274/wi18/readings/course29sig01.pdf
Describes the ARNOLD renderer employing randomized quasi-Monte Carlo sampling using low discrepancy sequences for pixel sampling, global illumination, area light sampling, motion blur, depth of field, etc.

[5] E. Veach, December, Robust Monte Carlo Methods for Light Transport Simulation, Ph. D. dissertation for Stanford University, 1997, pp. 58-65
An online version can be found at http://graphics.stanford.edu/papers/veach_thesis/
Includes a description of low discrepancy sequences, quasi-Monte Carlo sampling and its application to solving the global illumination problem.

[6] L. Szirmay-Kalos, Importance Driven Quasi-Monte Carlo Walk Solution of the Rendering Equation, Winter School of Computer Graphics Conf., 1998
An online version can be found at http://www.fsz.bme.hu/~szirmay/imp1_link.html
Describes a two-pass method for solving the global illumination problem employing quasi-Monte Carlo sampling, as well as importance sampling using low discrepancy sequences.